介绍

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。迪杰斯特拉算法采用的是贪心策略，将Graph中的节点集分为最短路径计算完成的节点集S和未计算完成的节点集T，每次将从T中挑选V0->Vt最小的节点Vt加入S，并更新V0经由Vt到T中剩余节点的更短距离，直到T中的节点全部加入S中，它贪心就贪心在每次都选择一个距离源点最近的节点加入最短路径节点集合。迪杰斯特拉算法只支持非负权图，它计算的是单源最短路径，即单个源点到剩余节点的最短路径，时间复杂度为O(n²)。

算法流程

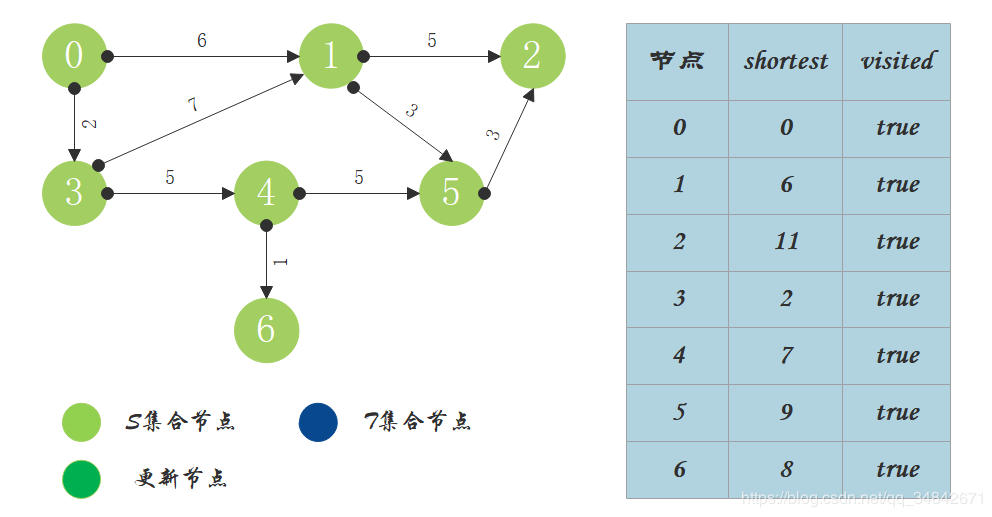
本节将对算法流程进行模拟，设置Graph为包含7个顶点和9条边的有向无环图，源点为0，计算从源点0到剩余节点的最短路径，Graph如下：

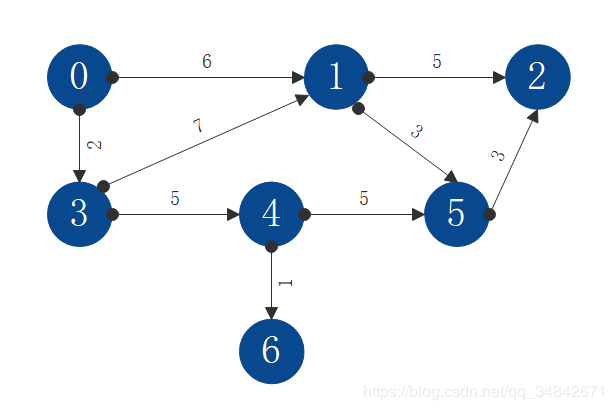
每个节点将维护shortest和visited两个数据结构，shortest存储v0到该节点的最短路径，visited存储v0到该节点的最短路径是否求出。S为已求出最短路径的节点，T为未求出最短路径的节点。源节点只允许将S中的节点作为中间节点来计算到达其它节点的最短路径，不允许将T中的节点作为中间节点来计算到达其它节点的最短路径。随着S中节点的增加，源节点可达的节点才会增加。初始状态下，源节点只可达节点1和节点3。

算法步骤如下：

1. 将源节点（即节点0）加入S中，对shortest和visited数组进行更新。
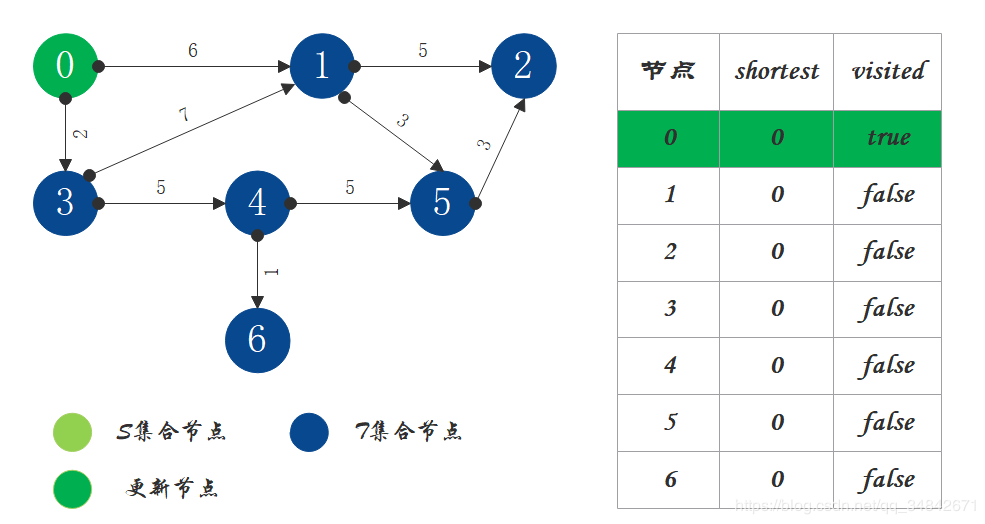
2. S中现有节点0，源节点可达T中的节点1和节点3，节点0->节点1距离为6，节点0->节点3距离为2，按距离从小到大排序，因此选择将节点3加入S中。更新源点将节点3作为中间节点到达其它节点的距离。
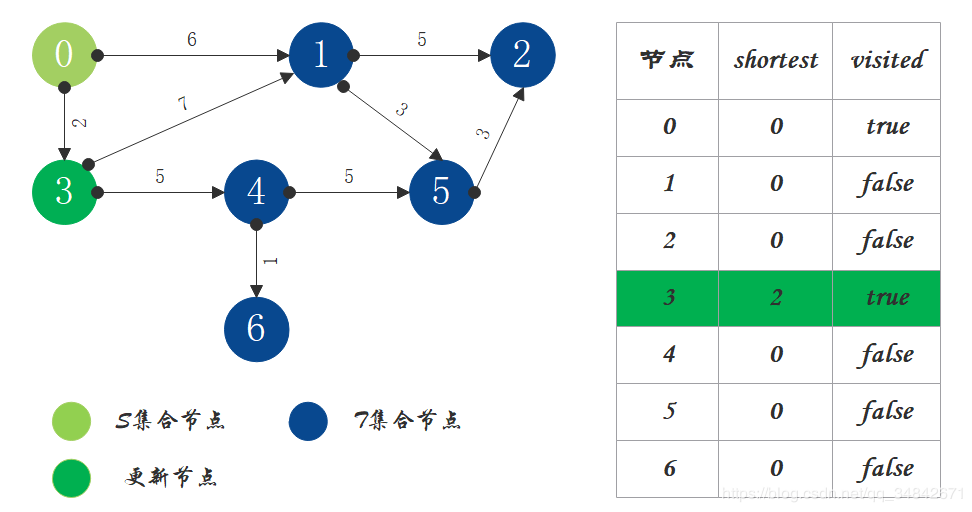
3. S中现有节点0和节点3，源节点可达T中的节点1和4，节点0->节点1距离为6，节点0->节点4距离为7，按距离从小到大排序，因此选择将节点1加入S中。更新源点将节点1作为中间节点到达其它节点的距离。
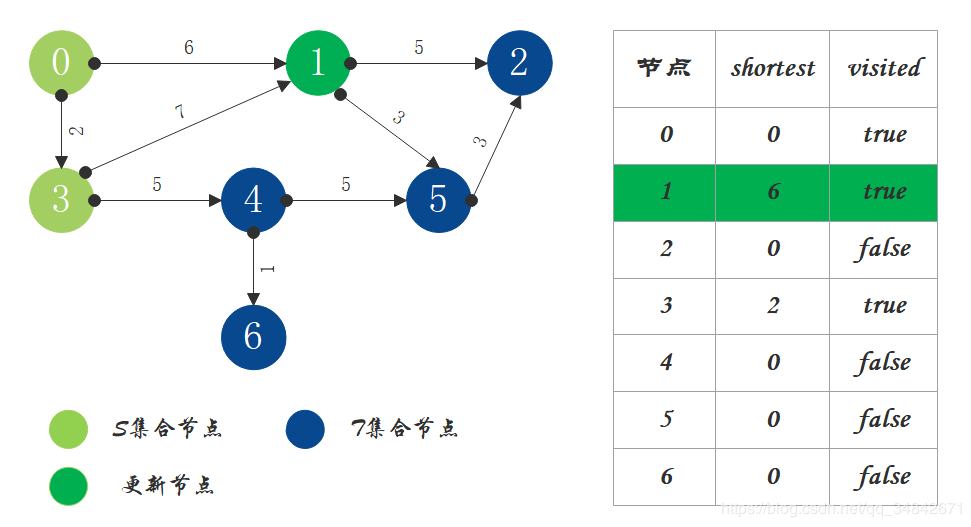
4. S中现有节点0、1、3，源节点可达T中的节点2、4、5，0->2距离为11，0->4距离为7，0->5距离为9，按距离从小到大排序，因此选择将节点4加入S中。更新源点将节点4作为中间节点到达其它节点的距离。
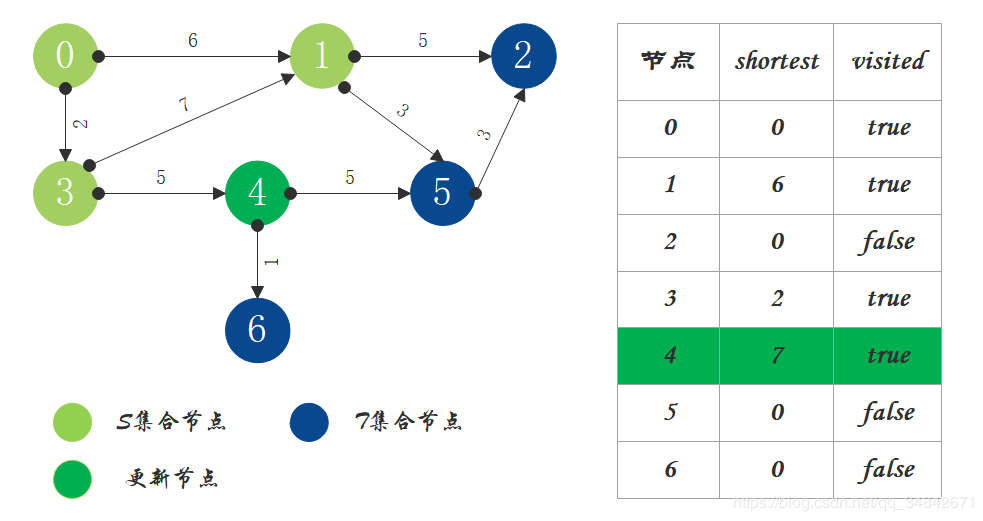
5. S中现有节点0、1、3、4，源节点可达T中的节点2、5、6，0->2距离为11，0->5距离为9，0->6距离为8，按距离从小到大排序，因此选择将节点6加入S中。更新源点将节点6作为中间节点到达其它节点的距离。
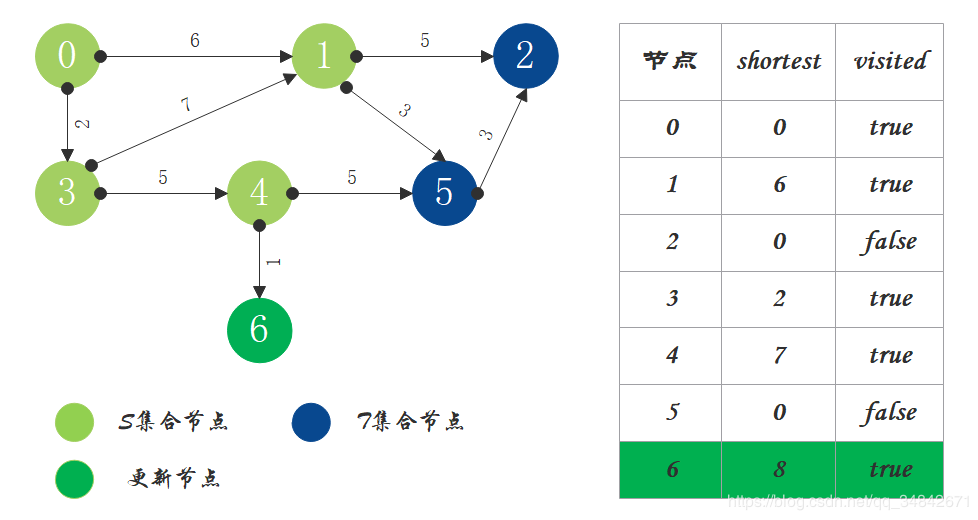
6. S中现有节点0、1、3、4、6，源节点可达T中的节点2、5，0->2距离为11，0->5距离为9，按距离从小到大排序，因此选择将节点5加入S中。更新源点将节点5作为中间节点到达其它节点的距离。
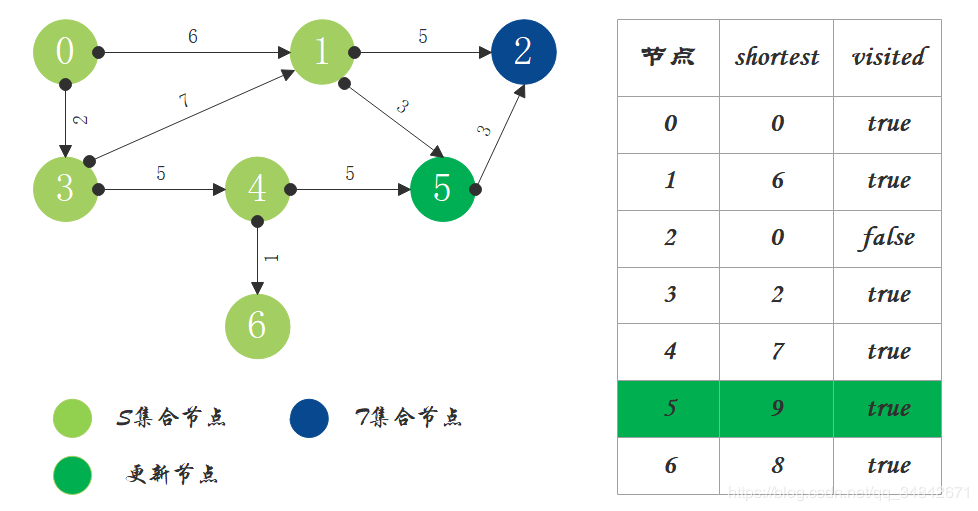
7. T中只剩下节点2，0->2距离为11，将节点2加入S中。
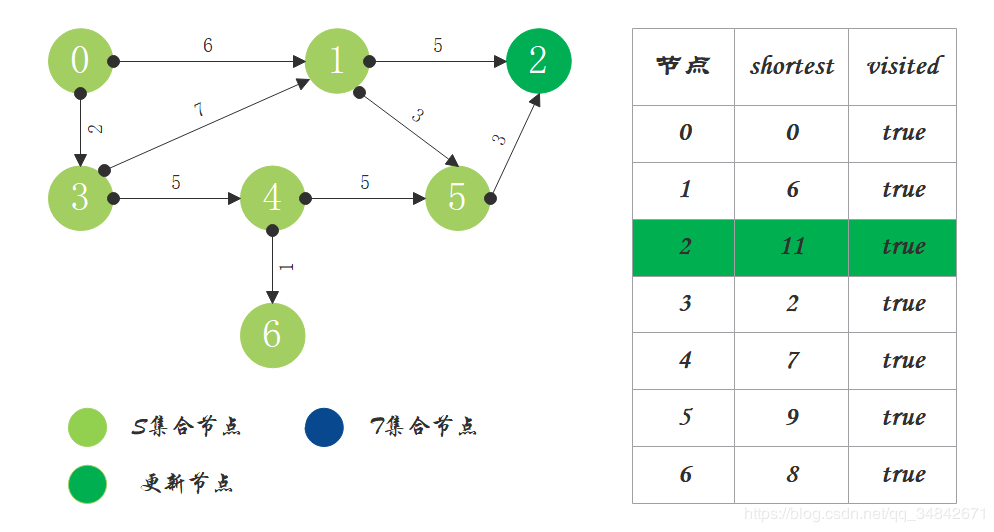
8. 算法结束，源点到其它节点的最短路径都已依次求出。

Java实现

public static void dijstra(int[][] matrix, int source) {
    //最短路径长度
    int[] shortest = new int[matrix.length];
    //判断该点的最短路径是否求出
    int[] visited = new int[matrix.length];
    //存储输出路径
    String[] path = new String[matrix.length];

    //初始化输出路径
    for (int i = 0; i < matrix.length; i++) {
        path[i] = new String(source + "->" + i);
    }

    //初始化源节点
    shortest[source] = 0;
    visited[source] = 1;

    for (int i = 1; i < matrix.length; i++) {
        int min = Integer.MAX_VALUE;
        int index = -1;

        for (int j = 0; j < matrix.length; j++) {
            //已经求出最短路径的节点不需要再加入计算并判断加入节点后是否存在更短路径
            if (visited[j] == 0 && matrix[source][j] < min) {
                min = matrix[source][j];
                index = j;
            }
        }

        //更新最短路径
        shortest[index] = min;
        visited[index] = 1;

        //更新从index跳到其它节点的较短路径
        for (int m = 0; m < matrix.length; m++) {
            if (visited[m] == 0 && matrix[source][index] + matrix[index][m] < matrix[source][m]) {
                matrix[source][m] = matrix[source][index] + matrix[index][m];
                path[m] = path[index] + "->" + m;
            }
        }

    }

    //打印最短路径
    for (int i = 0; i < matrix.length; i++) {
        if (i != source) {
            if (shortest[i] == MaxValue) {
                System.out.println(source + "到" + i + "不可达");
            } else {
                System.out.println(source + "到" + i + "的最短路径为：" + path[i] + "，最短距离是：" + shortest[i]);
            }
        }
    }
}

转自：图解最短路径之迪杰斯特拉算法（Java实现） (opens new window)