 常用查找算法及Java实现
常用查找算法及Java实现
# 常用算法
# 顺序查找
顺序查找也称为线形查找,属于无序查找算法。从数据结构线形表的一端开始,顺序扫描,依次将扫描到的结点关键字与给定值k相比较,若相等则表示查找成功;若扫描结束仍没有找到关键字等于k的结点,表示查找失败。
顺序查找的时间复杂度为O(n)。
public class Search {
public static void main(String[] args) {
int arr[] = {5, 11, 7, 9, 2, 3, 12, 8, 6, 1, 4, 10};
search(arr,3);
}
/**
* 顺序查找
*/
public static int order(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i;
}
}
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 二分查找
也称为是折半查找,属于有序查找算法。用给定值k先与中间结点的关键字比较,中间结点把线形表分成两个子表,若相等则查找成功;若不相等,再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表,这样递归进行,直到查找到或查找结束发现表中没有这样的结点。
最坏情况下,关键词比较次数为log2(n+1),且期望时间复杂度为O(log2n);
/**
* 常规二分查找
*/
public static int half(int[] arr, int target) {
//使数组有序
Arrays.sort(arr);
System.out.println(String.format("原数组%s中查找【%s】", Arrays.toString(arr), target));
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = ((right - left) >> 1) + left;
if (target > arr[mid]) {
left = mid + 1;
} else if (target < arr[mid]) {
right = mid - 1;
} else {
return mid;
}
}
return -1;
}
/**
* 递归二分查找
* @param high len-1
*/
public static int halfByRecurse(int[] arr, int target, int low, int high) {
int mid = ((high - low) >> 1) + low;
if (low == high) {
return -1;
}
if (target == arr[mid]) {
return mid;
}
if (target > arr[mid]) {
return halfByRecurse(arr, target, mid + 1, high);
}
if (target < arr[mid]) {
return halfByRecurse(arr, target, low, mid - 1);
}
return -1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 插值查找
基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。当然,差值查找也属于有序查找 代码基本上和二分查找一样,有修改的地方就是mid的获取
在二分查找中 可改写成 $mid =low + $ $ {high-low} \over {2}$
也就是说我们的mid每次都是折中的取,但是对于一些均匀分布的有序表,这样做感觉有些费时,比如找字典的时候,找a这个字母,我们肯定不会从中间开始,而是偏向于字典前面一些开始。
插值查找就是基于这样的思想 我们对1/2进行改进:
key就是要查找的值,数组a是有序表
简单的理解就是计算出key所占比,然后更好地找到key所在的区间范围 但是对于极端分布的数组,插值查找的效率就大打折扣了 比如
int a[7]={0,1,2,100,102,1000,10000}
Java代码实现
/**
* 插值查找
*/
public static int insert(int[] arr, int target) {
//使数组有序
Arrays.sort(arr);
System.out.println(String.format("原数组%s中进行插值查找【%s】", Arrays.toString(arr), target));
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) * ((target - arr[left]) / (arr[right] - arr[left]));
if (target > arr[mid]) {
left = mid + 1;
} else if (target < arr[mid]) {
right = mid - 1;
} else {
return mid;
}
}
return -1;
}
/**
* 递归插值查找
*
* @param high len-1
*/
public static int insertByRecurse(int[] arr, int target, int low, int high) {
int mid = low + (high - low) * ((target - arr[low]) / (arr[high] - arr[low]));
if (low <= high) {
if (target == arr[mid]) {
return mid;
} else if (target > arr[mid]) {
return insertByRecurse(arr, target, mid + 1, high);
} else {
return insertByRecurse(arr, target, low, mid - 1);
}
} else {
return -1;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 斐波那契查找
斐波那契查找原理: 该查找原理与二分查找和插值查找类似,仅仅改变中间节点middle位置,middle位置不再是中间或插值得到,而是位于黄金分割点附近,即mid = low + F(k - 1) - 1(F,斐波那契数列)。
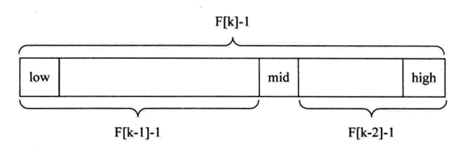
F(k-1)-1的说明
- 由斐波那契数列F[k]=F[k-1] + F[k-2],可以得到F[k]-1=(F[k-1]-1) + (F[k-2]-1)+1。说明只要顺序表的长度为F[k]-1,则可以-将顺序表分成长度为F[k-1]-1和F[k-2]-1的两段,即中间位置为:mid=low+F[k-1]-1。
- 类似的每个字段也可以用相同的方式进行分割。
- 可能顺序表长度n不一定等于F[k]-1,需要将原来的顺序表长度n增加至F[k]-1。(k值只要使得F[k]-1大于或等于n)。
/**
* @author blog.unclezs.com
* @date 2020/7/31 19:00
*/
public class FibonacciSearch {
public static void main(String[] args) {
int[] array = {1, 8, 10, 89, 1000, 1234};
int index = fibonacciSearch(array, 1);
if(-1 == index) {
System.err.println("没有找到");
} else {
System.out.println("找到,位置:" + index);
}
}
/**
* 斐波那契查找
*/
public static int fibonacciSearch(int[] array, int key) {
int length = array.length;
int low = 0;
int high = length - 1;
// 斐波那契分割数的索引
int k = 0;
int mid = 0;
// 找到有序表元素个数在斐波那契数列中最接近的最大数列值
while(high > (fibonacci(k) - 1)) {
k++;
}
// 补齐有序表
int [] tmpArray = Arrays.copyOf(array, fibonacci(k));
for(int i = length; i < tmpArray.length; i++) {
tmpArray[i] = array[high];
}
while(low <= high) {
mid = low + fibonacci(k - 1) - 1;
// 查找值小于中值,在小的那一部分继续查找
if(key < tmpArray[mid]) {
high = mid - 1;
k--;
}
// 查找值大于中值,在大的那一部分继续查找
else if(key > tmpArray[mid]) {
low = mid + 1;
k -= 2;
} else {
// 可能存在补齐列表
return Math.min(mid, high);
}
}
return -1;
}
/**
* 动态规划实现斐波那契数列
*
* @param n /
* @return /
*/
public static int fibonacci(int n) {
if (n <= 1) {
return n;
}
int pre1 = 0;
int pre2 = 1;
int total = pre1 + pre2;
for (int i = 2; i <= n; i++) {
total = pre1 + pre2;
pre1 = pre2;
pre2 = total;
}
return total;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
# 树表查找
# 二叉查找树
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后在就行和每个节点的父节点比较大小,查找最适合的范围。 这个算法的查找效率很高,但是如果使用这种查找方法要首先创建树。
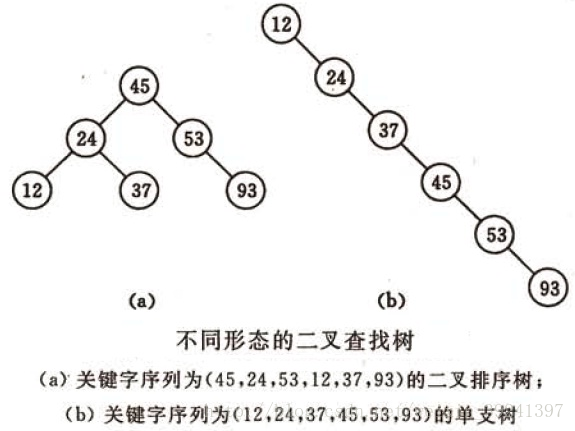
对二叉查找树进行中序遍历即可得到一个有序的列表。
对这个方面还有升级版本的红黑树,来保证平衡
# 平衡查找树之2-3查找树(2-3 Tree)
和二叉树不一样,2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node),他保存1个key和左右两个自己点。对应3节点(3-node),保存两个Key。
2-3查找树的定义如下:
- 要么为空,要么:
- 对于2节点,该节点保存一个key及对应value,以及两个指向左右节点的节点,左节点也是一个2-3节点,所有的值都比key要小,右节点也是一个2-3节点,所有的值比key要大。
- 对于3节点,该节点保存两个key及对应value,以及三个指向左中右的节点。左节点也是一个2-3节点,所有的值均比两个key中的最小的key还要小;中间节点也是一个2-3节点,中间节点的key值在两个跟节点key值之间;右节点也是一个2-3节点,节点的所有key值比两个key中的最大的key还要大。
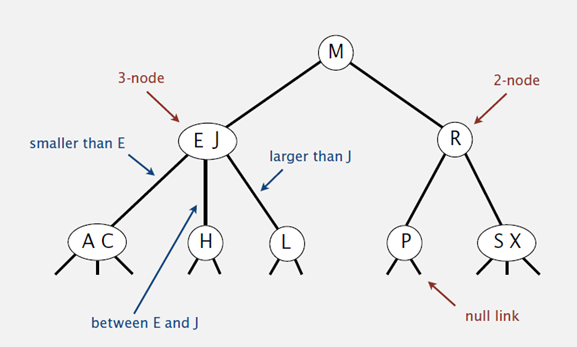
# 分块查找
分块查找又称索引顺序查找,它是顺序查找的一种改进方法。
算法思想:将n个数据元素"按块有序"划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须"按块有序";即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都必须小于第3块中的任一元素,……
算法流程:
- 先选取各块中的最大关键字构成一个索引表;
- 查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后,在已确定的块中用顺序法进行查找。
# 哈希查找
我们使用一个下标范围比较大的数组来存储元素。可以设计一个函数(哈希函数, 也叫做散列函数),使得每个元素的关键字都与一个函数值(即数组下标)相对应,于是用这个数组单元来存储这个元素;也可以简单的理解为,按照关键字为每一个元素"分类",然后将这个元素存储在相应"类"所对应的地方。但是,不能够保证每个元素的关键字与函数值是一一对应的,因此极有可能出现对于不同的元素,却计算出了相同的函数值,这样就产生了"冲突",换句话说,就是把不同的元素分在了相同的"类"之中。后面我们将看到一种解决"冲突"的简便做法。
总的来说,"直接定址"与"解决冲突"是哈希表的两大特点。