介绍

BFS（广度优先遍历，Breadth First Search）及DFS（深度优先遍历，Depth First Search）是遍历树或图的两种最常用的方法。

深度优先算法

算法描述

深度优先算法是从起始顶点开始，递归访问其所有邻近节点，比如A节点是其第一个邻近节点，而B节点又是A的一个邻近节点，则DFS访问A节点后再访问B节点，如果B节点有未访问的邻近节点的话将继续访问其邻近节点，否则继续访问A的未访问邻近节点，当所有从A节点出去的路径都访问完之后，继续递归访问除A以外未被访问的邻近节点。

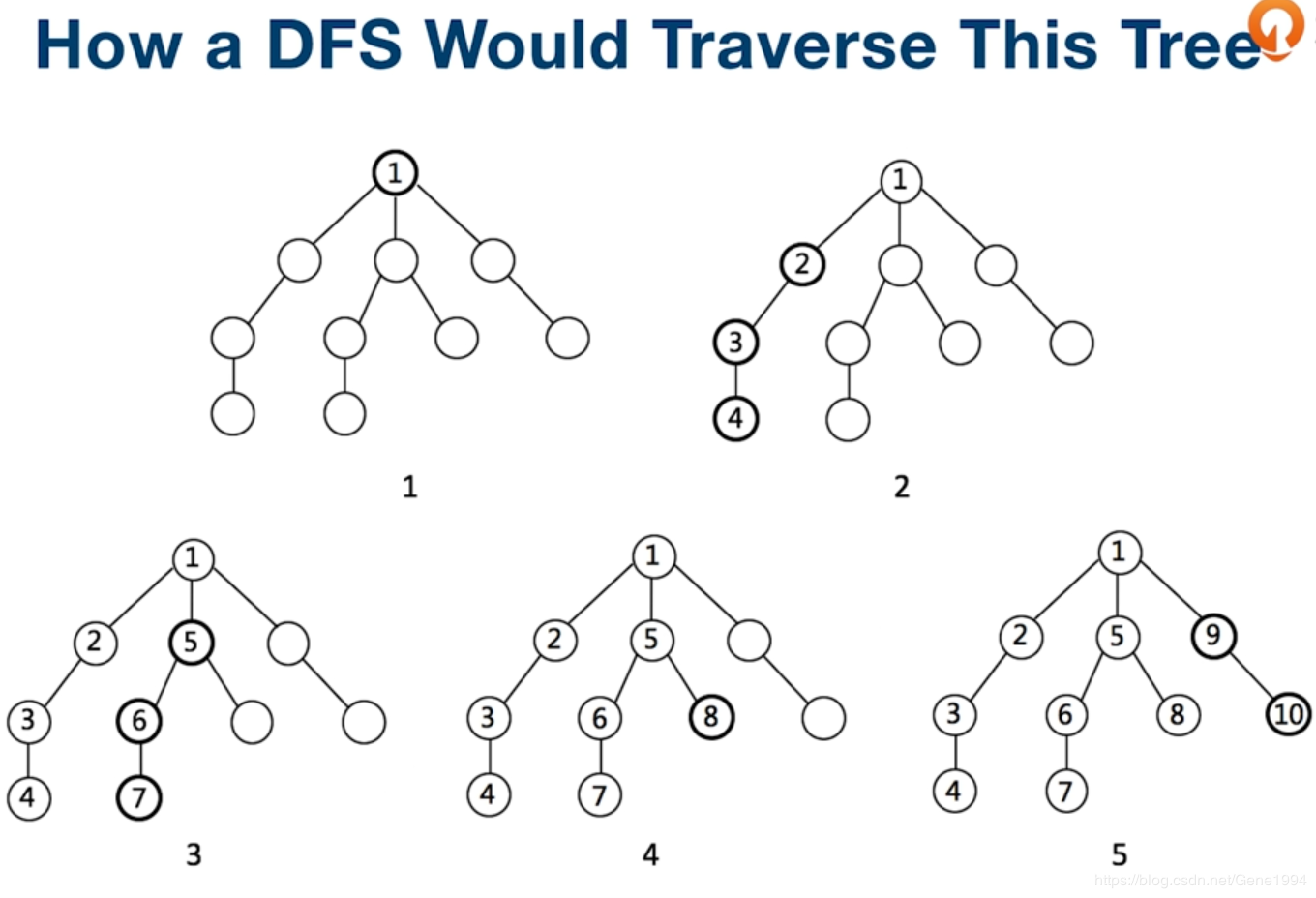
Java实现

可以用递归和栈实现，时间复杂度为O(N)。

  public class DFS {
    static class TreeNode {
        TreeNode left;
        TreeNode right;
        int data;

        public TreeNode(int data) {
            this.data = data;
        }
    }

    public static void main(String[] args) {
        TreeNode root = new TreeNode(-1);
        root.left = new TreeNode(10);
        root.right = new TreeNode(5);
        root.right.left = new TreeNode(2);
        root.left.left = new TreeNode(3);
        root.left.left.left = new TreeNode(4);
        dfsByRecursion(root);
        dfsByStack(root);
    }

    /**
     * 递归实现DFS
     *
     * @param node 树节点
     */
    public static void dfsByRecursion(TreeNode node) {
        if (node != null) {
            System.out.println(node.data);
            if (node.left != null) {
                dfsByRecursion(node.left);
            }
            if (node.right != null) {
                dfsByRecursion(node.right);
            }
        }
    }

    /**
     * 栈实现
     * @param node 节点
     */
    public static void dfsByStack(TreeNode node) {
        Stack<TreeNode> nodes = new Stack<>();
        nodes.push(node);
        while (!nodes.isEmpty()) {
            TreeNode treeNode = nodes.pop();
            System.out.println(treeNode.data);
            if (treeNode.right != null) {
                nodes.push(treeNode.right);
            }
            if (treeNode.left != null) {
                nodes.push(treeNode.left);
            }
        }
    }
}
//-1，10，3，4，5，2

广度优先算法

算法描述

其主要思想是从起始点开始，将其邻近的所有顶点都加到一个队列（FIFO）中去，然后标记下这些顶点离起始顶点的距离为1.最后将起始顶点标记为已访问，今后就不会再访问。然后再从队列中取出最先进队的顶点A，也取出其周边邻近节点，加入队列末尾，最后离开这个顶点A。依次下去，直到队列为空为止。从上面描述的过程我们知道每个顶点被访问的次数最多一次（已访问的节点不会再访问）。

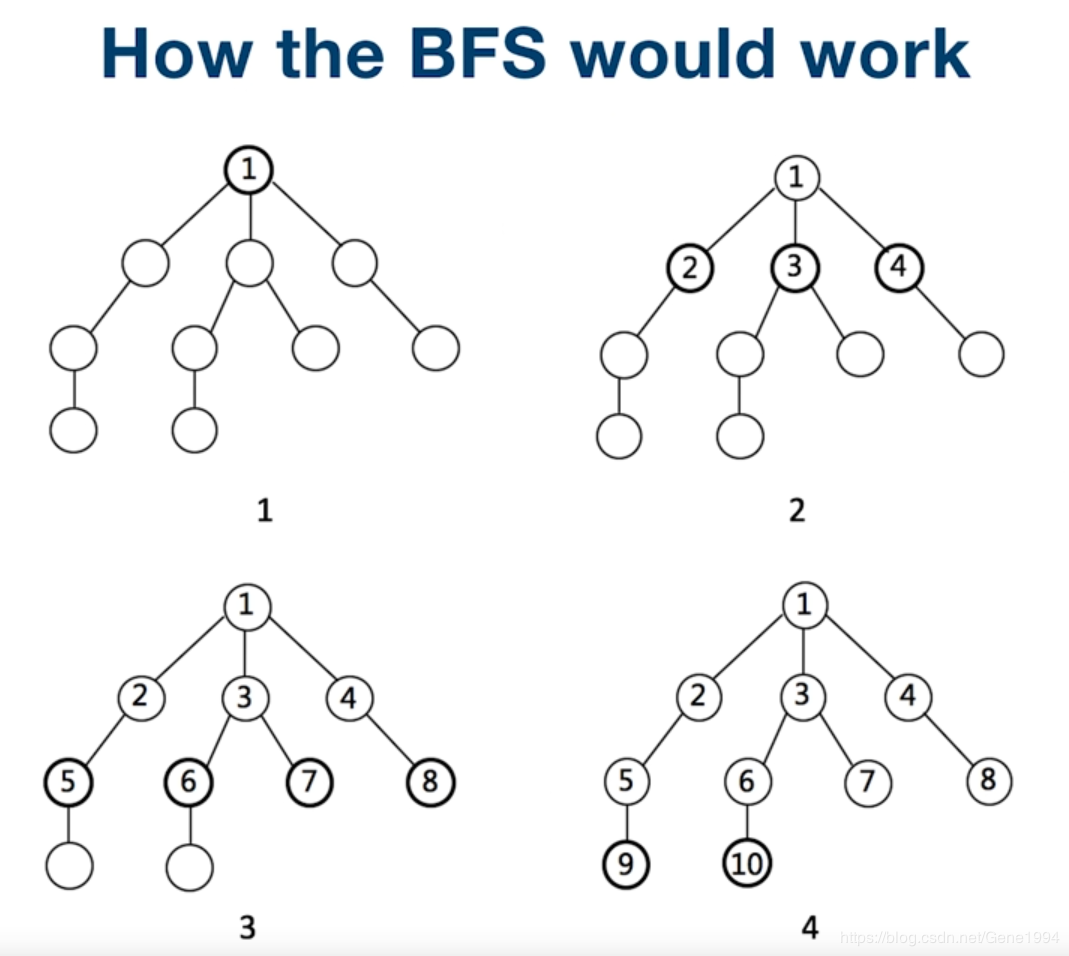
Java实现

通过队列实现，其中树节点和测试数据和DFS一样。时间复杂度为O(N)。

    /**
     * 队列实现 BFS
     * @param node 节点
     */
    public static void bfsByQueue(TreeNode node) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(node);
        while (!queue.isEmpty()) {
            TreeNode treeNode = queue.poll();
            System.out.println(treeNode.data);
            if (treeNode.left != null) {
                queue.add(treeNode.left);
            }
            if (treeNode.right != null) {
                queue.add(treeNode.right);
            }
        }
    }