一、红-黑树的性质

1.简述

jdk中的TreeMap是由红黑树实现的，所以本文记录下我分析的红黑树 红黑树实际是实现二叉排序树的实现自平衡的算法之一，所以可以叫红黑树为高级二叉查找树。 如果不了解排序树请先学习排序树

2.性质

1.每个节点不是红色就是黑色的； 2.根节点总是黑色的； 3.如果节点是红色的，则它的子节点必须是黑色的（反之不一定）； 4.从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）。

二、平衡化的旋转

为了达到树的平衡我们需要对其进行旋转，下面说的是左右旋的基本概念

1.左旋

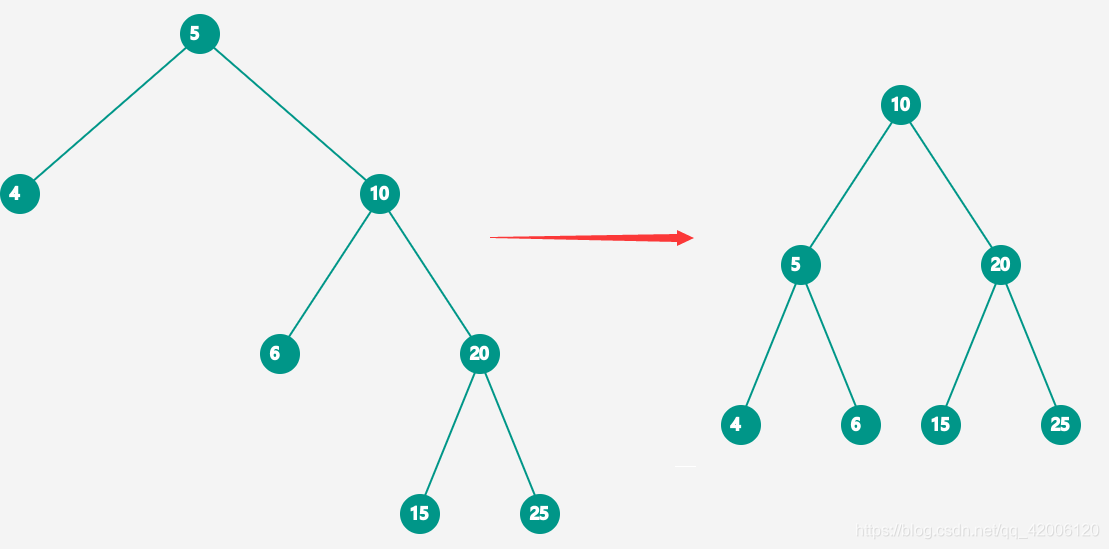
以5为节点进行左旋转 以E为节点进行左旋转示意图

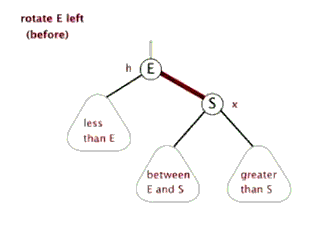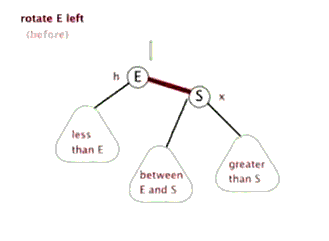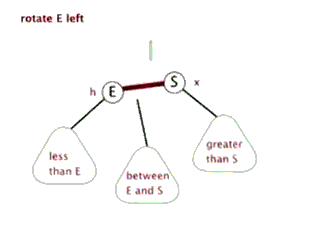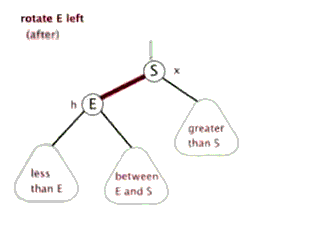
2.右旋

以20为节点进行右旋转

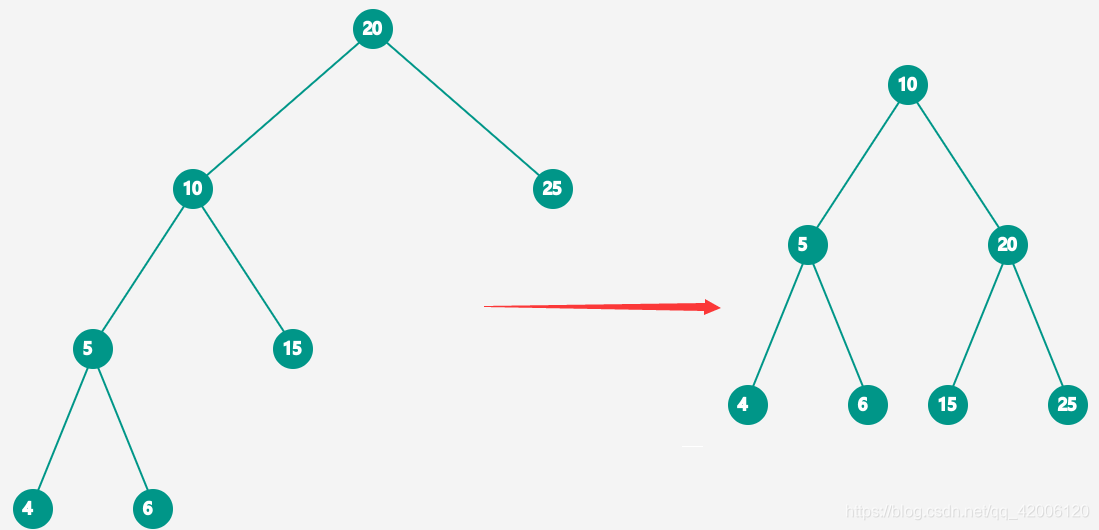以s为节点，右旋转示意图

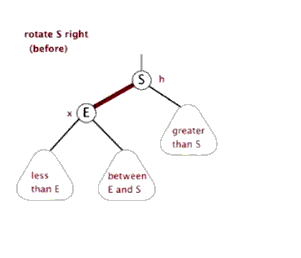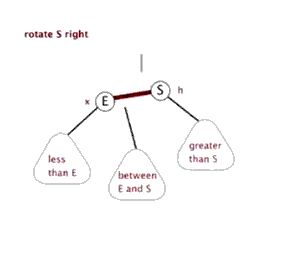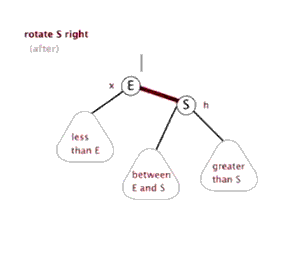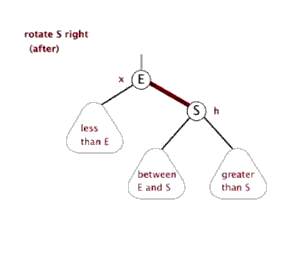
三、插入过程

插入的时候为保证红黑树性质不被改变，插入后应该对其旋转操作，需要修复红黑树结构的情况为父节点为红色的时候

1.情况分析

我按照两种情况来分析需要旋转的情况 新插入的节点默认都为红色

1.1.父亲在左边

1.1.1 .叔叔为红色 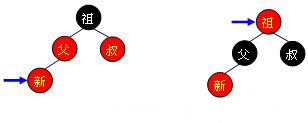这里不需要旋转，只需要换色即可，（父亲,叔叔）<--->（祖父)，再将祖父当作根节点判断是否满足红黑树结构再进行操作

1.1.2 叔叔为黑色、我在左 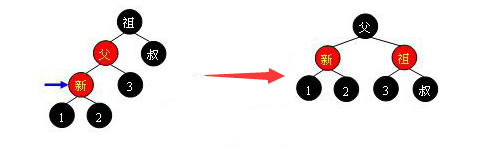这里只需要进行以父为节点右旋转，然后父亲->黑色，祖父->红色

1.1.3 叔叔为黑色、我在右边 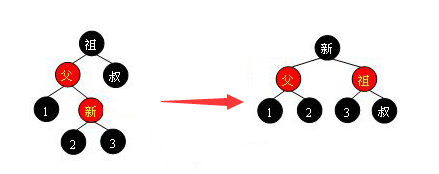这里要先对父节点做一次左旋，再以祖为节点右旋转

1.2.父亲在右边

1.2.1 叔叔为红色 和1.1.1一样 1.2.2 叔叔为黑色，我在左 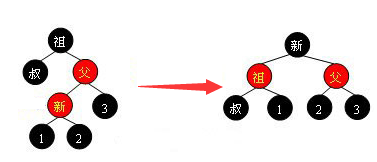这里需要以父为节点进行一次左旋，再以祖父为节点进行左旋转即可 1.2.1 叔叔为黑色，我在右 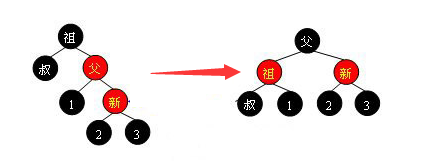这里只需要以祖为节点左旋一次即可达到平衡

2.源码分析

回到java源码中对TreeMap中插入时修复红黑树的方法为fixAfterInsertion 源码：

private void fixAfterInsertion(Entry<K,V> x) {
      me.color=RED;
        //x为根节点时候不需要操作，x父亲为黑色时为正确红黑树，不需要修复
        while (me!=null&&me!=root&&me.parent.color==RED){
            //分两大种情况处理，父亲在左边或者右边时
            if(parentOf(me)==leftOf(parentOf(parentOf(me)))){//父亲在左边的时候
                Node<E> uncle = rightOf(parentOf(parentOf(me)));//获取叔叔(在右)
                if(colorOf(uncle)==BLACK){//叔叔为黑色
                    //此时父左，叔右，若我为左则以祖父为根R旋转，若我在右边则以我为根进行LR转
                    if(rightOf(parentOf(me))==me){//我在右边
                        me=parentOf(me);
                        leftRotate(me);
                    }
                    setColor(parentOf(me),BLACK);
                    setColor(parentOf(parentOf(me)),RED);
                    rightRotate(parentOf(parentOf(me)));
                }else {//叔叔为红色,交换颜色（父亲,叔叔）<->（祖父），再将祖父接着前操作
                    setColor(parentOf(uncle),RED);//祖父红色
                    setColor(parentOf(me),BLACK);//父亲黑色
                    setColor(uncle,BLACK);//叔叔黑色
                    me=parentOf(uncle);//祖父为节点接着修复
                }
            }
            else {//父亲在右边的时候
                Node<E> uncle = leftOf(parentOf(parentOf(me)));//获取叔叔(在左)
                if(colorOf(uncle)==BLACK){//叔叔为黑色
                    //此时父右，叔左，若我为左则以我为根RL旋转，若我在右边则以祖父为根进行L转
                    if(leftOf(parentOf(me))==me){//我在左边
                        me=parentOf(me);
                        rightRotate(me);
                    }
                    setColor(parentOf(me),BLACK);
                    setColor(parentOf(parentOf(me)),RED);
                    leftRotate(parentOf(parentOf(me)));
                }else {//叔叔为红色,交换颜色（父亲,叔叔）<->（祖父），再将祖父接着前操作
                    setColor(parentOf(uncle),RED);//祖父红色
                    setColor(parentOf(me),BLACK);//父亲黑色
                    setColor(uncle,BLACK);//叔叔黑色
                    me=parentOf(uncle);//祖父为节点接着修复
                }
            }
        }
        root.color=BLACK;
    }