数据结构之堆Heap

定义

堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵完全二叉树的数组对象。 将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。

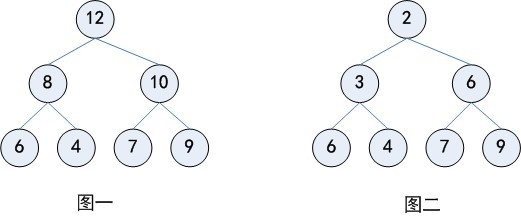
• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

图一为最大堆，图二为最小堆】

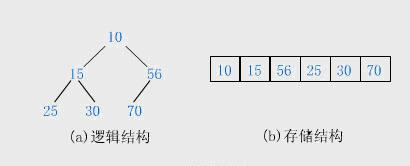
堆的存储结构

1. 根节点位置：根节点的数据总是在数组的位置[0]
2. 节点的父节点位置：假设一个非根节点的数据在数组中的位置[i]，那么它的父节点总是在位置[(i-1)/2]
3. 节点的孩子节点位置：假设一个节点的数据在数组中的位置为[i]，那么它的孩子（如果有）总是在下面的这两个位置：左孩子在[2 * i+1]，右孩子在[2 * i+2]

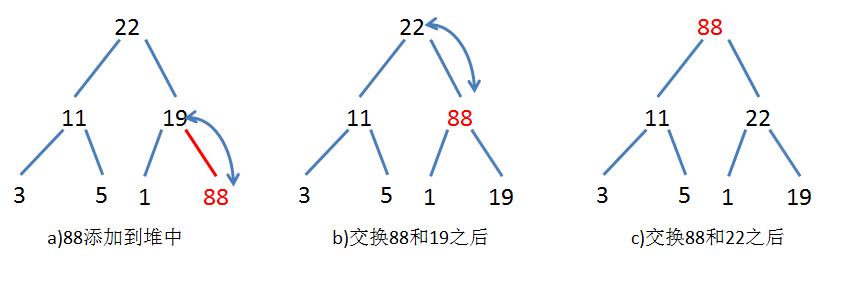
堆的一些操作

插入过程

1. 将新元素增加到堆的末尾
2. 按照优先顺序，将新元素与其父节点比较，如果新元素小于父节点则将两者交换位置。
3. 不断进行第2步操作，直到不需要交换新元素和父节点，或者达到堆顶则插入成功

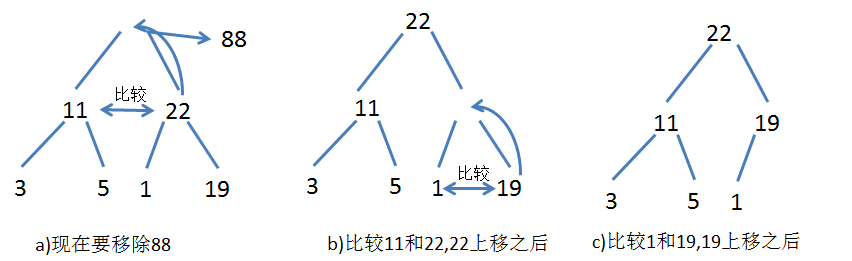
删除根过程

堆的删除操作与插入操作相反，插入操作从下往上调整堆，而删除操作则从上往下调整堆。

1. 删除堆顶元素（通常是将堆顶元素放置在数组的末尾）
2. 比较左右子节点，将小的元素上调。
3. 不断进行步骤2，直到不需要调整或者调整到堆底。

Java实现堆

大根堆

/**
 * @author blog.unclezs.com
 * @date 2020/7/27 22:15
 */
public class BigHeap {
    private final int[] data;
    private int size;

    public BigHeap(int length) {
        this.data = new int[length];
        Arrays.fill(this.data, -1);
    }

    public void add(int node) {
        this.data[size] = node;
        int currentIndex = size++;
        while (currentIndex > 0) {
            int parentIndex = (currentIndex - 1) / 2;
            //如果这个节点比父节点小
            if (data[currentIndex] > data[parentIndex]) {
                swap(currentIndex, parentIndex);
            } else {
                break;
            }
            currentIndex = parentIndex;
        }
    }

    @Override
    public String toString() {
        return Arrays.toString(data);
    }

    /**
     * 删除根
     *
     * @return 根
     */
    public int deleteRoot() {
        //堆尾元素放到根
        int root = data[0];
        data[0] = data[--size];
        data[size] = -1;
        int currentIndex = 0;
        for (; ; ) {
            int leftIndex = 2 * currentIndex + 1;
            int rightIndex = 2 * currentIndex + 2;
            //已经没有子节点了
            if (leftIndex > size) {
                break;
            }
            //如果有右子节点，并且大于左子节点
            if (rightIndex < size && data[rightIndex] > data[leftIndex]) {
                leftIndex = rightIndex;
            }
            if (data[leftIndex] > data[currentIndex]) {
                swap(leftIndex, currentIndex);
            }  else {
                break;
            }
            currentIndex = leftIndex;
        }
        return root;
    }

    private void swap(int from, int to) {
        int tmp = data[from];
        data[from] = data[to];
        data[to] = tmp;
    }

    public static void main(String[] args) {
        BigHeap heap = new BigHeap(10);
        heap.add(88);
        heap.add(11);
        heap.add(22);
        heap.add(3);
        heap.add(5);
        heap.add(1);
        heap.add(19);
        System.out.println(heap.deleteRoot());
        System.out.println(heap);
    }
}

小根堆

修改增加删除方法

    public void add(int node) {
        this.data[size] = node;
        int currentIndex = size++;
        while (currentIndex > 0) {
            int parentIndex = (currentIndex - 1) / 2;
            //如果这个节点比父节点小
            if (data[currentIndex] < data[parentIndex]) {
                swap(currentIndex, parentIndex);
            } else {
                break;
            }
            currentIndex = parentIndex;
        }
    }

    @Override
    public String toString() {
        return Arrays.toString(data);
    }

    /**
     * 删除根
     *
     * @return 根
     */
    public int deleteRoot() {
        //堆尾元素放到根
        int root = data[0];
        data[0] = data[--size];
        data[size] = -1;
        int currentIndex = 0;
        for (; ; ) {
            int leftIndex = 2 * currentIndex + 1;
            int rightIndex = 2 * currentIndex + 2;
            //已经没有子节点了
            if (leftIndex > size) {
                break;
            }
            //如果有右子节点，并且小于左子节点
            if (rightIndex < size && data[rightIndex] < data[leftIndex]) {
                leftIndex = rightIndex;
            }
            if (data[leftIndex] < data[currentIndex]) {
                swap(leftIndex, currentIndex);
                currentIndex = leftIndex;
            }  else {
                break;
            }
        }
        return root;
    }

参考

1. 数据结构-堆和堆的Java实现 (opens new window)
2. 数据结构之堆的定义 (opens new window)
3. 数据结构-堆的实现 (opens new window)