 数据结构之树Tree
数据结构之树Tree
# 树的概念
树状图是一种数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个结点有零个或多个子结点;
- 没有父结点的结点称为根结点;
- 每一个非根结点有且只有一个父结点;
- 除了根结点外,每个子结点可以分为多个不相交的子树
# 满二叉树
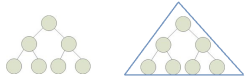
⼀个⼆叉树,如果每⼀个层的结点数都达到最⼤值,则这个⼆叉树就是满⼆叉树。也就是说,如果⼀个⼆叉树的层数为K,且结点总数是(2^k) -1 ,则它就是满⼆叉树。
- 一个层数为k 的满二叉树总结点数为:。因此满二叉树的结点数一定是奇数个。
- 第i层上的结点数为:
- 一个层数为k的满二叉树的叶子结点个数(也就是最后一层):2^(k-1)
# 完全二叉树
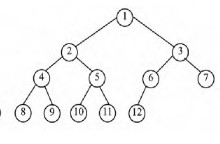
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
- 如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
- 如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空;则该节点之后的队列中的结点都为叶子节点;该树才是完全二叉树,否则就不是完全二叉树;
# 二叉查找树(Binary Search Tree)
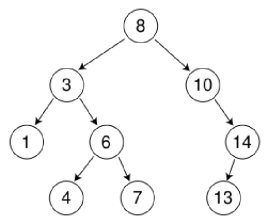
也叫二叉搜索树、二叉排序树。 ⼆叉查找树的特点:
- 若任意节点的左⼦树不空,则左⼦树上所有结点的 值均⼩于它的根结点的值;
- 若任意节点的右⼦树不空,则右⼦树上所有结点的值均⼤于它的根结点的值;
- 任意节点的左、右⼦树也分别为⼆叉查找树;
- 没有键值相等的节点(no duplicate nodes)。
顺序表做储存的二叉查找树: 按数组下标进行存储,根节点存储在下标0处,其左孩子存储于下标2 0 + 1,右孩子存储于下标2 0 + 2 …依次类推。 下标为i的节点,左右孩子存储于下标2 * i + 1与2 * i + 2
# 平衡⼆叉树(Self-balancing binary search tree)
平衡二叉树(Balanced Binary Tree)又被称为AVL树(有别于AVL算法),且具有以下性质:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间,不过相对二叉查找树来说,时间上稳定了很多。
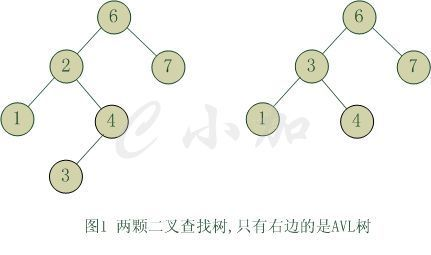
推荐阅读:一文读懂平衡二叉树 (opens new window)
# 红黑树
- 每个节点⾮红即⿊;
- 根节点总是⿊⾊的;
- 每个叶⼦节点都是⿊⾊的空节点(NIL节点);
- 如果节点是红⾊的,则它的⼦节点必须是⿊⾊的(反之不⼀定);
- 从根节点到叶节点或空⼦节点的每条路径,必须包含相同数⽬的⿊⾊节点(即相同的⿊⾊⾼度)。
为什么要⽤红⿊树? 简单来说红⿊树就是为了解决⼆叉查找树的缺陷,因为⼆叉查找树在某些情况下会退化成⼀个线性结 构。
推荐阅读:
# 哈夫曼树
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
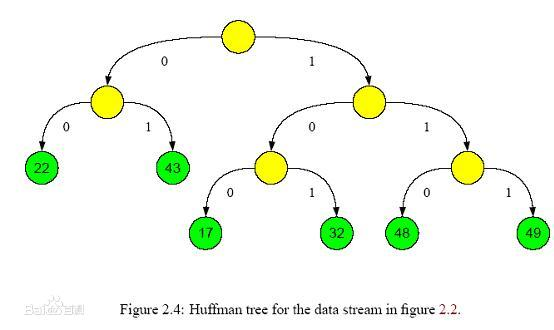
推荐阅读:漫画:什么是 “哈夫曼树” ? (opens new window) 推荐阅读:数据结构——树——哈夫曼树 (opens new window)
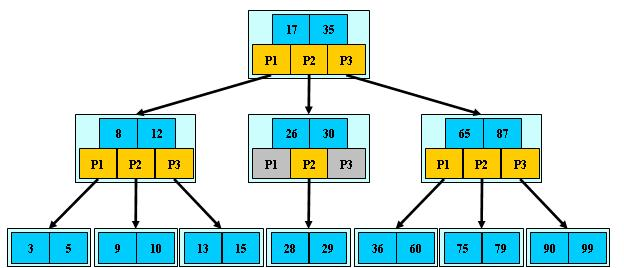
# B树(B-树)
# B树性质
- 根结点至少有两个子女;
- 每个非根节点所包含的关键字个数 j 满足:(m/2) - 1 <= j <= m - 1;
- 除根结点以外的所有结点(不包括叶子结点)的度数正好是关键字总数加1,故内部子树个数 k 满足:(m/2) <= k <= m ;
- 所有的叶子结点都位于同一层。
# B树特点
- B-tree是一种多路搜索树(并不是二叉的),对于一棵M阶树:
- 定义任意非叶子结点最多只有M个孩子;且M>2;
- 根结点的孩子数为[2, M],除非根结点为叶子节点;
- 除根结点以外的非叶子结点的儿子数为[M/2, M];
- 非叶子结点的关键字个数=指向儿子的指针个数-1;
- 每个非叶子结点存放至少M/2-1(取上整)和至多M-1个关键字;
- 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
- 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
- 所有叶子结点位于同一层;
# 推荐阅读
# B+树
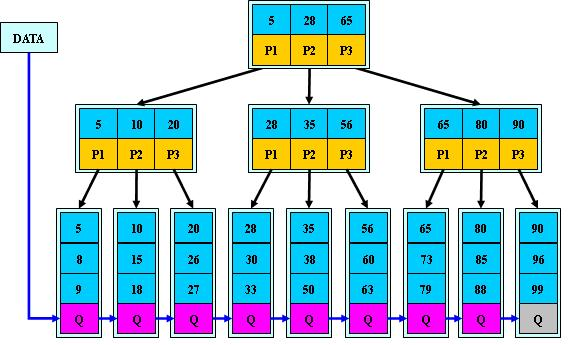
B+ 树是一种树数据结构,是一个n叉树,每个节点通常有多个孩子,一棵B+树包含根节点、内部节点和叶子节点。根节点可能是一个叶子节点,也可能是一个包含两个或两个以上孩子节点的节点。
# 特点
其定义基本与B-树同,除了:
非叶子结点的子树指针与关键字个数相同;
非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
为所有叶子结点增加一个链指针;
所有关键字都在叶子结点出现;
# 应用
B+ 树通常用于数据库和操作系统的文件系统中。NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系统都在使用B+树作为元数据索引。B+ 树的特点是能够保持数据稳定有序,其插入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入。
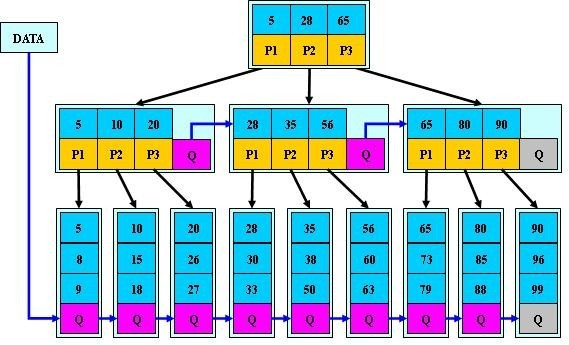
# B*树
B*-tree是B+-tree的变体,在B+树的基础上(所有的叶子结点中包含了全部关键字的信息,及指向含有这些关键字记录的指针),B*树中非根和非叶子结点再增加指向兄弟的指针;
B*树定义了非叶子结点关键字个数至少为(2/3)*M,即块的最低使用率为2/3(代替B+树的1/2)。
# 关于B树类的文章
- 二叉树学习笔记之B树、B+树、B*树 (opens new window)
- B-树,B+树,B*树详解 (opens new window)
- B-树,B+树与B*树的优缺点比较 (opens new window)
# LSM树(Log-Structured Merge Tree)
存储引擎和B树存储引擎一样,同样支持增、删、读、改、顺序扫描操作。而且通过批量存储技术规避磁盘随机写入问题。当然凡事有利有弊,LSM树和B+树相比,LSM树牺牲了部分读性能,用来大幅提高写性能。
因为B+树可能存在大量得随机IO访问
推荐阅读:LSM树由来、设计思想以及应用到HBase的索引 (opens new window)
# 树的遍历
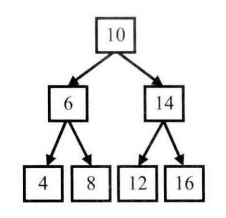
- 前序遍历:先访问根节点,再访问左子节点,最后访问右子节点。图中的二叉树的前序遍历的顺序是10、6、4、8、14、12、16。
- 中序遍历:先访问左子节点,再访问根节点,最后访问右子节点。图中的二叉树的中序遍历的顺序是4、6、8、10、12、14、16。
- 后序遍历:先访问左子节点,再访问右子节点,最后访问根节点。图中的二叉树的后序遍历的顺序是4、8、6、12、 16、14、10。