 跳越表
跳越表
# 介绍
跳跃表是一种有序的数据结构,它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。
# 跳跃表
# 什么是跳跃表
对于一个单链表来讲,即便链表中存储的数据是有序的,如果我们要想在其中查找某个数据,也只能从头到尾遍历链表。这样查找效率就会很低,时间复杂度会很高,是 O(n)。
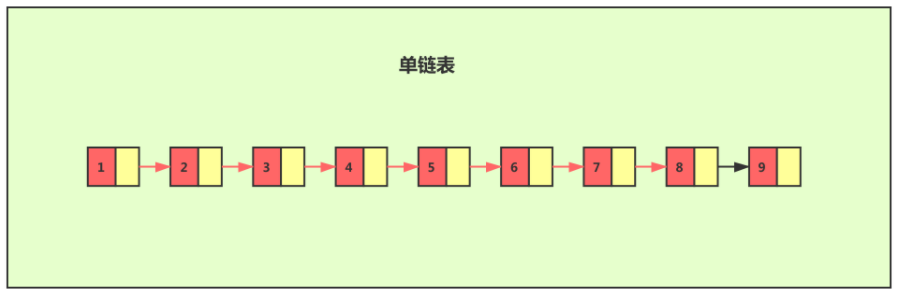
如果我们想要提高其查找效率,可以考虑在链表上建索引的方式。每两个结点提取一个结点到上一级,我们把抽出来的那一级叫作索引。
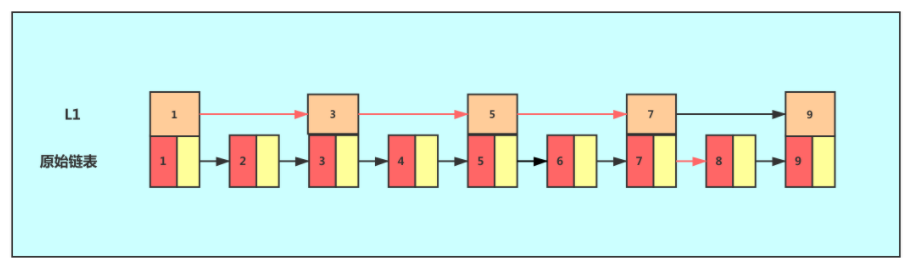
这个时候,我们假设要查找节点8,我们可以先在索引层遍历,当遍历到索引层中值为 7 的结点时,发现下一个节点是9,那么要查找的节点8肯定就在这两个节点之间。我们下降到链表层继续遍历就找到了8这个节点。原先我们在单链表中找到8这个节点要遍历8个节点,而现在有了一级索引后只需要遍历五个节点。
从这个例子里,我们看出,加来一层索引之后,查找一个结点需要遍的结点个数减少了,也就是说查找效率提高了,同理再加一级索引。
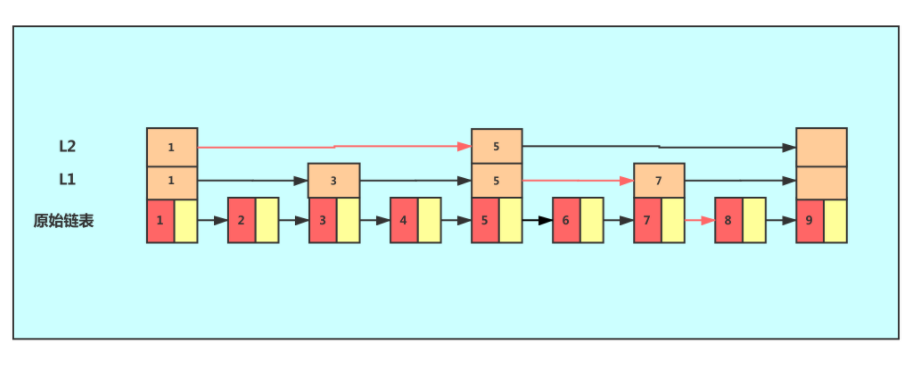
这次次数更少了,只需要3次即可查找到数字8,可以看出来,增加更多的索引可以增加查找速度。
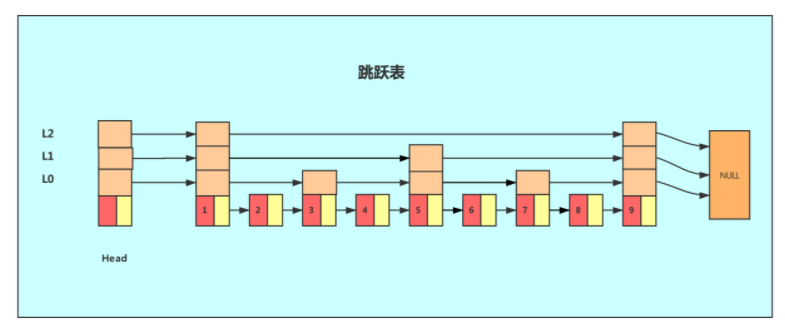
上面就是跳跃表了。
# 时间复杂度O(logn)
有n个结点的链表,假设每两个链表构建一个索引,那么: 第一级索引个数为:n/2; 第二级索引个数为:n/4; ··· 第h级索引个数为:n/2^h; 现在假设最后一级索引的个数为2 ,则h +1 = logn,算上最底下的一层链表,那么这个跳表的高度H= logn。
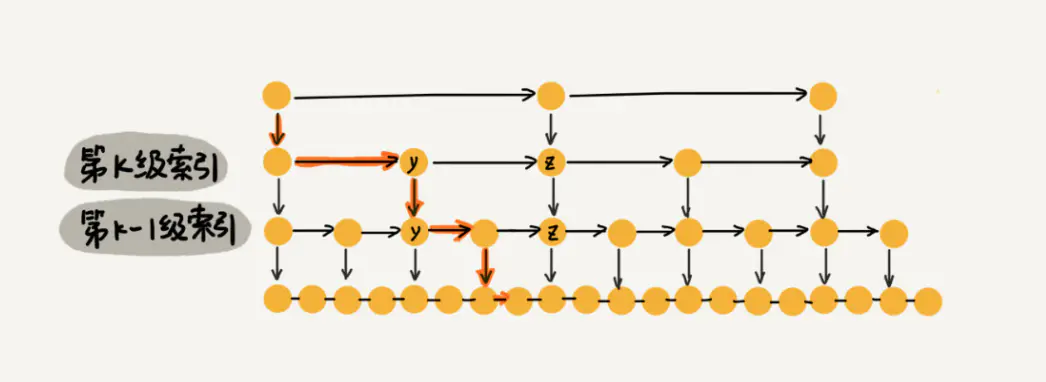
在图里,我们想查找x,在第k级,遍历到y结点,发现x大于y,但x小于y后面的结点z,所以先顺着y往下到第k-1级,发现y,z之间有三个节点,所以我们在k-1级索引中,遍历3个节点找到x,以此类推,在每一层需要通过3个节点找目标数,那么总的时间复杂度就为O(3*logn),因为3是常数,所以最后的时间复杂度为O(logn)。 这一结构相当于让跳表实现了二分查找,只是建立这么多的索引是否会浪费空间呢?我们来看一下跳表的空间复杂度。
# 跳表的空间复杂度O(n)
还是回到刚刚的例子,我们可以发现,链表上的索引数目按第一层,第二层,···,倒数第二层,最后一层的顺序排列下来分别为:n/2,n/4,···,4,2,观察到了吗?就是一个等比数列,计算该跳表的空间复杂度,相当于给等比数列求和,等比数列求和公式:
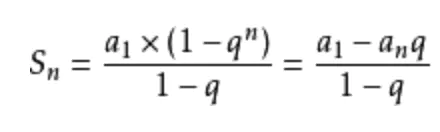
顺着公式依次带入:a1=n/2,an= 2,q=1/2,求得Sn= n-2,所以空间复杂度为O(n),与此同时,我们顺便考虑一下每三个节点抽取一个索引的情况,还是依据刚刚的思路,发现Sn= n-1/2,空间复杂度将近缩减了一半。 总之,跳表就是空间换时间的那个思路,但如果链表中存储的对象很大时,其实索引占用的这些空间对整个来说是可以忽略不计的。
# 跳表的高效插入和删除
# 插入
单链表在知道删除的节点是谁时,时间复杂度为O(1),因为跳表底层的单链表是有序的,为了维护这种有序性,在插入前需要遍历链表,找到该插入的位置,单链表遍历查找的时间复杂度是O(n),同理可得,跳表的遍历也是需要遍历索引数,所以是O(logn)。
# 删除
删除的节点要分两种情况:
- 删除的节点还在索引中,那删除时不仅要删除单链表中的节点,还要删除索引中的节点;
- 删除的节点只在链表中,不在索引中,那只需要删除链表中的节点即可。
# 特点
- 时间换空间
- 基于单链表加索引方式提升查找性能
# Redis中的跳跃表
Redis使用跳跃表作为有序集合键的底层实现之一,如果一个有序集合包含的元素数量比较多,又或者有序集合中元素的成员是比较长的字符串时, Redis就会使用跳跃表来作为有序集合健的底层实现。
这里我们需要思考一个问题——为什么元素数量比较多或者成员是比较长的字符串的时候Redis要使用跳跃表来实现?
从上面我们可以知道,跳跃表在链表的基础上增加了多级索引以提升查找的效率,但其是一个空间换时间的方案,必然会带来一个问题——索引是占内存的。原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值值和几个指针,并不需要存储对象,因此当节点本身比较大或者元素数量比较多的时候,其优势必然会被放大,而缺点则可以忽略。
# Redis中跳跃表的实现
Redis的跳跃表由zskiplistNode和skiplist两个结构定义,其中 zskiplistNode结构用于表示跳跃表节点,而 zskiplist结构则用于保存跳跃表节点的相关信息,比如节点的数量,以及指向表头节点和表尾节点的指针等等。
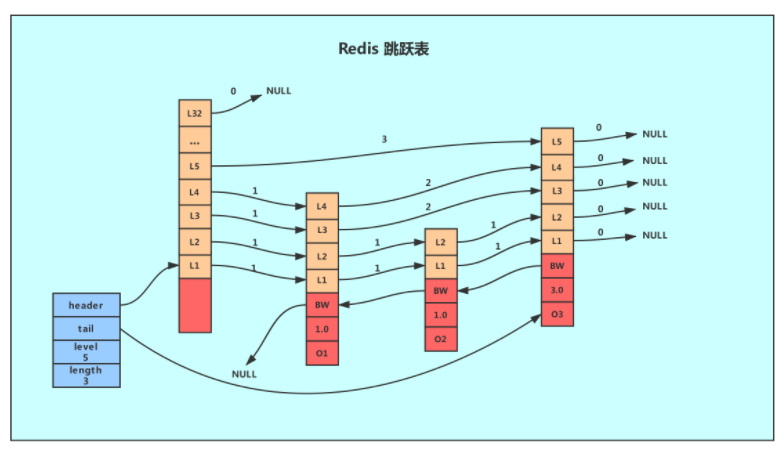
# skiplist结构
图左边第一个就是。
- header:指向跳跃表的表头节点,通过这个指针程序定位表头节点的时间复杂度就为O(1)
- tail:指向跳跃表的表尾节点,通过这个指针程序定位表尾节点的时间复杂度就为O(1)
- level:记录目前跳跃表内,层数最大的那个节点的层数(表头节点的层数不计算在内),通过这个属性可以再O(1)的时间复杂度内获取层高最好的节点的层数。
- length:记录跳跃表的长度,也即是,跳跃表目前包含节点的数量(表头节点不计算在内),通过这个属性,程序可以再O(1)的时间复杂度内返回跳跃表的长度。
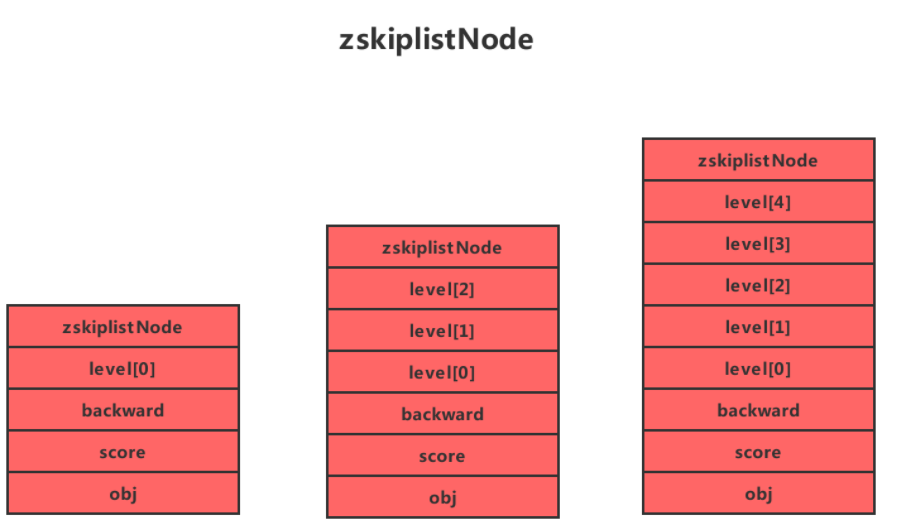
# zskiplistNode结构
图右边四个
层(level): 节点中用L1、L2、L3等字样标记节点的各个层,L1代表第一层,L代表第二层,以此类推。 每个层都带有两个属性:前进指针和跨度。前进指针用于访问位于表尾方向的其他节点,而跨度则记录了前进指针所指向节点和当前节点的距离(跨度越大、距离越远)。在上图中,连线上带有数字的箭头就代表前进指针,而那个数字就是跨度。当程序从表头向表尾进行遍历时,访问会沿着层的前进指针进行。 每次创建一个新跳跃表节点的时候,程序都根据幂次定律(powerlaw,越大的数出现的概率越小)随机生成一个介于1和32之间的值作为level数组的大小,这个大小就是层的“高度”。
后退(backward)指针: 节点中用BW字样标记节点的后退指针,它指向位于当前节点的前一个节点。后退指针在程序从表尾向表头遍历时使用。与前进指针所不同的是每个节点只有一个后退指针,因此每次只能后退一个节点。
分值(score): 各个节点中的1.0、2.0和3.0是节点所保存的分值。在跳跃表中,节点按各自所保存的分值从小到大排列。
成员对象(oj): 各个节点中的o1、o2和o3是节点所保存的成员对象。在同一个跳跃表中,各个节点保存的成员对象必须是唯一的,但是多个节点保存的分值却可以是相同的:分值相同的节点将按照成员对象在字典序中的大小来进行排序,成员对象较小的节点会排在前面(靠近表头的方向),而成员对象较大的节点则会排在后面(靠近表尾的方向)。
# 与红黑树对比
- 插入速度非常快速,因为不需要进行旋转等操作来维护平衡性
- 更容易实现
- 支持范围查找
- 跳表更加灵活,可以通过改变索引构建策略,有效平衡执行效率和内存消耗。
# 总结
跳跃表就是一个单链表存储数据,多个链表当作索引,不断进行2分建立索引,这样有点类似二分查找的样子。效率比较高。