Gossip protocol 也叫 Epidemic Protocol （流行病协议），实际上它还有很多别名，比如：“流言算法”、“疫情传播算法”等。

概念

Gossip 过程是由种子节点发起，当一个种子节点有状态需要更新到网络中的其他节点时，它会随机的选择周围几个节点散播消息，收到消息的节点也会重复该过程，直至最终网络中所有的节点都收到了消息。这个过程可能需要一定的时间，由于不能保证某个时刻所有节点都收到消息，但是理论上最终所有节点都会收到消息，因此它是一个最终一致性协议。

假设

1. Gossip 是周期性的散播消息，把周期限定为 1 秒

2. 被感染节点随机选择 k 个邻接节点（fan-out）散播消息，这里把 fan-out 设置为 3，每次最多往 3 个节点散播。

3. 每次散播消息都选择尚未发送过的节点进行散播

4. 收到消息的节点不再往发送节点散播，比如 A -> B，那么 B 进行散播的时候，不再发给 A。

注意：Gossip 过程是异步的，也就是说发消息的节点不会关注对方是否收到，即不等待响应；不管对方有没有收到，它都会每隔 1 秒向周围节点发消息。异步是它的优点，而消息冗余则是它的缺点。

这里一共有 16 个节点，节点 1 为初始被感染节点，通过 Gossip 过程，最终所有节点都被感染：

上图是 Gossip 传播过程的示意图，根据示意图和 Gossip 的过程描述，我们很容易发现 Gossip 对网络节点的连通性和稳定性几乎没有任何要求，它一开始就将网络某些节点只能与一部分节点部分连通 (opens new window)（Partially Connected Network）而不是以全连通网络 (opens new window)（Fully Connected Network）作为前提；能够容忍网络上节点的随意地增加或者减少，随意地宕机或者重启，新增加或者重启的节点的状态最终会与其他节点同步达成一致。Gossip 把网络上所有节点都视为平等而普通的一员，没有任何中心化节点或者主节点的概念，这些特点使得 Gossip 具有极强的鲁棒性，而且非常适合在公众互联网中应用。

优缺点

优点

扩展性

网络可以允许节点的任意增加和减少，新增加的节点的状态最终会与其他节点一致。

容错

网络中任何节点的宕机和重启都不会影响 Gossip 消息的传播，Gossip 协议具有天然的分布式系统容错特性。

去中心化

Gossip 协议不要求任何中心节点，所有节点都可以是对等的，任何一个节点无需知道整个网络状况，只要网络是连通的，任意一个节点就可以把消息散播到全网。

一致性收敛

Gossip 协议中的消息会以一传十、十传百一样的指数级速度在网络中快速传播，因此系统状态的不一致可以在很快的时间内收敛到一致。消息传播速度达到了 logN。

简单

Gossip 协议的过程极其简单，实现起来几乎没有太多复杂性。

缺点

分布式网络中，没有一种完美的解决方案，Gossip 协议跟其他协议一样，也有一些不可避免的缺陷，主要是两个：

消息的延迟

由于 Gossip 协议中，节点只会随机向少数几个节点发送消息，消息最终是通过多个轮次的散播而到达全网的，因此使用 Gossip 协议会造成不可避免的消息延迟。不适合用在对实时性要求较高的场景下。

消息冗余

Gossip 协议规定，节点会定期随机选择周围节点发送消息，而收到消息的节点也会重复该步骤，因此就不可避免的存在消息重复发送给同一节点的情况，造成了消息的冗余，同时也增加了收到消息的节点的处理压力。而且，由于是定期发送，因此，即使收到了消息的节点还会反复收到重复消息，加重了消息的冗余。

三种机制

直接邮寄（direct mail）

每个节点更新都会立即从其变更节点邮寄通知到所有其他节点。

机制	时间复杂度	网络流量	优点	缺点
直接邮寄（direct mail）	O(n)，n为节点数	1mn，m为更新消息数，n为节点数	更新效率高	不完全可靠，存在信息传递丢失风险

对于直接邮寄（direct mail） 这种方式，主要是当节点有数据更新便开始遍历节点池，遍历发送其他所有节点消息来通知自身节点数据的更新情况，实现算法较为简单。由于是一次性遍历通知，在遇到网络通信故障、节点宕机之后恢复等现实情况时没有办法容错和补偿，这是较为致命性的地方，因此极端情况下它是无法保证分布式环境下各节点数据一致性的。

反熵传播（anti-entropy）

概念

每个节点都会定期随机选择节点池中的一些节点，通过交换数据内容来解决两者之间的任何差异。

反熵传播（anti-entropy）中的节点只有两种状态，病原（Suspective）和感染（Infective），因此称作SI模型，一般叫做简易流行病（simple epidemics） 。 反熵传播（anti-entropy）的消息数量非常庞大，且无限制；通常只用于新加入节点的数据初始化。

机制	时间复杂度	网络流量	优点	缺点
反熵（anti-entropy）	O(log2n)，n为节点数	O((m*n)t)，n为节点数，m为更新消息数，t为周期数	1.可靠 2.定时重复 3.可容错	1.消息冗余 2.消息延迟 3.网络流量耗费较多

对于反熵（anti-entropy） 这种方式，和直接邮寄（direct mail）相比的最大特点就是解决了消息丢失无法补偿容错导致的数据无法保持一致的致命问题。它通过单点的定时随机通知周边节点进行数据交互的方式保持各节点之间数据的一致性。这里需要注意的是，一致性的保持是在节点数据变更后一段时间内通过节点间的数据交互逐渐完成的最终一致，并且由于每个节点都定期广播数据到周边随机的一部分节点，因此在数据交互上是存在冗余和延迟的。

伪代码实现

伪代码中围绕两个boolean变量：push、pull，表示同步消息模式。运行过程可分为两个线程理解：

• 异步消息同步线程，即消息同步入口，每个∆时间单位执行一次。
• 消息处理线程，即接收到消息，进行处理。

1. 本次数据同步发起者，记为A，A生成随机集合P。
2. 如果是push模式，并且A处于infected，则A发送数据给集合P。
   • 第11行，集合P收到数据，保存数据。同时意味着自己处于infected
3. 如果是pull模式，则A发送请求更新的指令给集合P。
   • 第15行，集合P收到请求更新的指令，如果自己处于infected，则发送第11行所保存的数据给A。
   • A接收到数据，即第11行。

实际应用

算法描述中，虽然描述的是周期性的向其他节点交换数据来消除两者之间的差异。但是反熵在实际生产中的应用和原本的描述会有所出入，主要原因包含两点：

1. 每次推送和拉取都是全量数据进行比较，性能消耗比较大。
2. 可能出现极端情况（两个节点互相进行推拉，其他的节点也没有选择它们两进行推拉）导致某些节点数据可能达不到一致。
3. 随机性的选择节点消除两者的差异，如果要整个集群节点都达到一致，所需时间不确定，也没有明确的标准表明集群中数据达到一致。

在实际应用场景中，不推荐采用随机的节点进行反熵。而是需要刻意的设计一个闭环，这样能在一个确定的时间范围内完成最终一致性，而不是基于随机的概率。

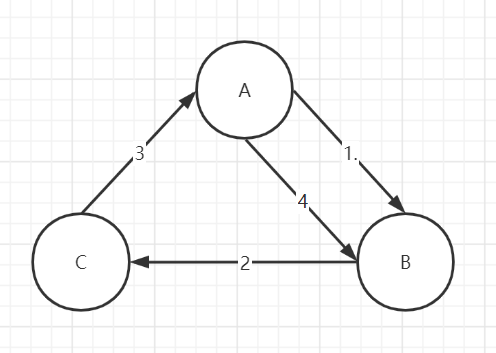
1. 由A发起反熵，A的数据推给B，可以把A中包含的数据B中不包含的数据同步给B
2. B的数据推给C，消除C中没有A、B的数据
3. C的数据推给A，则可以消除A中没有B、C的数据
4. A还需要再推一次给B，这样才能把C中的数据推给B

至此，完成数据的最终一致性。这里可以做一个优化：如果反熵每次都推送全量数据进行比较，太消耗资源。这里建议记录已完成一致性的数据，后续执行反熵，只推送增量数据。

谣言传播（rumor mongering）

概念

这里先以谣言传播方式来讲解分布式节点数据交互如下：

• 所有的节点在最开始没有产生数据变更时都假设是未知状态，它是不知道任何谣言信息的
• 当节点收到其他节点更新数据通知时，相当于听到了一条谣言，并将其视为热门开始传播给周边节点
• 当某个节点谣言盛行时，它会定期随机选择其他节点，并确保另一个节点知道
• 当某个节点发现周边节点都知道这个谣言时，该节点将停止将该谣言视为热点，并保留更新，而不会进一步传播

谣言传播周期可能比反熵周期更频繁，因为它们在每个站点所需要的资源更少，但是有可能更新不会到达所有站点。

谣言传播（rumor mongering）中的节点状态有Suspective(病原)、Infective(感染)、Removed(愈除)，因此称作SIR模型，一般叫做复杂流行病（complex epidemics） 。

• 消息生产节点即为Suspective(病原)状态
• 消息接收节点即为Infective(感染)状态，会进行消息传播
• 节点接收消息后即为Removed(愈除)状态，不再进行传播

消息只包含最新更新数据，消息在某个时间点之后会被标记为Removed(愈除)状态，并且不再被传播，通常用于节点间数据增量同步。

机制	时间复杂度	网络流量	优点	缺点
谣言传播（rumor mongering）	O(log2n)，n为总节点数	O((m*n)t)，n为节点数(递减)，m为更新消息数，t为周期数	1.可靠 2.定时重复 3.可容错	1.消息冗余 2.消息延迟 3.网络流量耗费较多

伪代码实现

1. 本次数据同步发起者，记为A，A生成随机集合P。
2. 如果是push模式，并且A处于infected，则A发送更新数据给集合P。
   • 集合P收到更新数据，第16行，判断是否已处理该数据，则返回feedback给A。
   • 如果处理，则保存该更新数据。同时意味着自己处于infected
3. 如果是pull模式，则发送请求更新的指令给集合P。
   • 第23行，集合P收到请求更新的指令，如果自己处于infected，则发送第19行所保存的更新数据给A。
   • A接收到更新数据，即第15行。
4. A收到feedback消息，通过概率切换到removed

实际应用

谣言传播，可以快速的向网络中广播，非常具有传染性，适合节点数量多、集群庞大的网络中更新数据。由于集群中都是对等节点，它比较适合动态变化的分布式系统。

但是为了方便谣言传播，发送的数据包不能太大，主要用于新数据增量更新。

通讯模式

在 Gossip 协议下，网络中两个节点之间有三种通信方式:

• Push: 节点 A 将数据 (key,value,version) 及对应的版本号推送给 B 节点，B 节点更新 A 中比自己新的数据
• Pull：A 仅将数据 key, version 推送给 B，B 将本地比 A 新的数据（Key, value, version）推送给 A，A 更新本地
• Push/Pull：与 Pull 类似，只是多了一步，A 再将本地比 B 新的数据推送给 B，B 则更新本地

如果把两个节点数据同步一次定义为一个周期，则在一个周期内，Push 需通信 1 次，Pull 需 2 次，Push/Pull 则需 3 次。虽然消息数增加了，但从效果上来讲，Push/Pull 最好，理论上一个周期内可以使两个节点完全一致。直观上，Push/Pull 的收敛速度也是最快的。

复杂度分析

对于一个节点数为n的网络来说，假设每个周期p内，新感染的节点都能再感染至少一个新节点，那么感染节点数与周期规律如下

周期	新感染数	总感染数
p1	1	2
p2	2	4
p3	4	8
p4	8	16
pN	2n-1	2n

时间复杂度 那么Gossip协议将变成一个二叉树查找，经过log2(n) 个周期之后，感染全网，时间开销是O(log2(n)) 。

消息复杂度 由于每个周期，每个节点都会至少发出一次消息，因此，消息复杂度是 O(N2) 。这里也可以理解为是网络交互或网络通信消耗的空间复杂度。

以上Gossip 理论上最优的收敛速度，但是在实际情况中，最优的收敛速度是很难达到的。

可以去这个网站模拟下：gossip 模拟 (opens new window)

实际应用

基于 Gossip 协议的一些有名地方：

• Apache Cassandra
• Redis（Cluster模式）
• Consul
• BitCoin

可以看看 gossip 的 java 实现 jgossip (opens new window)